Graph Theory - Shake hand problem - Combinatorics 01

Story:

Mr. Bean, Mrs. Bean and five couples meet in a party.

They greet by shaking hands to each other iff they have not seen each other beforehand. They hug each other otherwise.

Mr. Bean says, if not include himself, there are no one in the party who has shaken hand the same number of times.

Ask: How many times Mrs. Bean has shake hand to?

Solution

There will be 10 people in the party.

Define 10 nodes: Y0, Y1, ..., Y8 and Mr.Bean.

Y0 := the one who has shake-hand to no one,

Y1 := the one who has shake-hand to 1 of others,

...

No one shake hand to oneself.

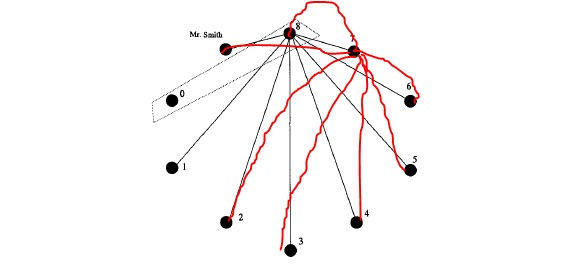
The Algorithm

1. Y8 has shaken hand to 8 of them - i.e. the 8 ones has at least 1 hand-shake - but not 1 of them, whom must be Y0. Y8 and Y0 must be couple.

Note that 8 edges Y8-Y1, Y8-Y2, ..., Y8-Y7 and Y8-Mr.Bean are formed.

2. Y7 has shaken hand to 7 of others, but not 2 of them. The two of them must be Y0 and Y1. Known that Y0 is couple of Y8. Besides, Y1 has shaken hand to Y8 already. So, Y1 must be couple of Y7.

Note that Y2 has already shake hand to Y7 and Y8.

3. Y6 do not shake hand with Y0, Y1, Y2. Y0, Y1 are paired already. Y2 do not shake hand with Y6. Y6 must be couple of Y2.

4. By similar argument, Y5 must be couple of Y3.

5. Y4 left un-paired. Y4 must be a couple of Mr. Bean.

Therefore, Mrs. Bean has shake hand to 4 others.

The arguments can be illustrated by a graph of nodes and edges.